This article is about me learning how to optimize matrix multiplication on a GPU using PTX. The GPUs are computing device which the host machine offloads its workload, when it has to compute large data parallel task. Learning about its limitations and writing efficient GPU code is a good skill to have. NVIDIA GPUs are one of the industry leaders in this domain. Let’s see how we can write matmul code in NVIDIA’s GPU using its low-level instruction set. This was inspired by this article by Siboehm.

Introduction

Before diving into PTX, let us see how our code is first compiled into executable. There are two parts to GPU code, one part which specifies what the host (a.k.a. CPU) has to do, second part tells how the GPU has to function. The host part of the code, can be compiled using various language binding’s to CUDA and there are lots of various APIs available to do a lot of cool GPU-CPU stuff. Then we specify what each thread in GPU does via kernel function. This kernel function is written using C like language, and later it is lowered to Intermediate representation (IR) which is device-agnostic. This IR is referred to as PTX instruction set. Later this PTX code is compiled to device specific binary by driver and compilers. We will skip the writing the code is C like language and directly write the code in PTX to learn various aspects to it.

PTX brief overview

What is PTX ? It is a low level parallel thread execution (PTX) virtual machine and Instruction set architecture (ISA). This exposes GPU as a data parallel computing device. This enables multiple high level domain specific languages (DSLs) to write GPU programming code, some examples are Triton, CuTile etc. If you need to know basics of GPU programming read through CUDA Programming guide. The PTX allows us to specify information like blocks (using CTAs(Cooperative thread Arrays)), threads, grids and cooperative groups through cluster of CTAs. It also exposes different memory/address types using state spaces like registers, shared memory, global memory, texture etc. I am yet to explore all this, it sounds cool and interesting.

Matrix multiplication Setup

In this experiment, we will try to multiply two 8192 x 8192 matrices (i.e C = AB). This computation requires O(n^3) time complexity, which is approximately of the order 10^{21}. To check the correctness of our GPU kernel, we compare the matrix with numpy implementation. We measure mean absolute error, and it should be 1e-3. This kernels are not compatible with all dimensions of matrices, should work only for this configuration, as the goal is for my learning and simplifying the PTX code.

How to write a PTX kernel ?

First, you have to write the code in a string or text file (preferably with .ptx extension) using ASCII characters. You will have to figure out a way to bind the functions defined in the ptx file to the CUDA runtime via some APIs. I have my own skeleton code for it using pycuda python bindings. You can find my skeleton code here.

The ptx file should begin with the following line, it is mandatory if you want it to compiler properly. Note: you cannot add comments before this line.

.version 8.0
.target sm_86
.address_size 64

What do these values mean ?

  • .version : This tells which version of ptx we are using. This depends on the driver version of CUDA you are using.
  • .target sm_86 : This tells which target device we are compiling this ptx instruction into. It is sm_86 for my 3050 Mobile RTX GPU.
  • .address_size : This is if you are targeting 64bit address space. All the address computation is performed using u64 data type.

Then we make a visible function symbol with declaration of parameter type and names, so that the driver/compiler can link the function calls in host to these function in ptx. The body of the function will implement the logic in assembly like IR.

.visible .entry sgemm_naive(
    .param .u64 ptrA,
    .param .u64 ptrB,
    .param .u64 ptrOut,
    .param .u32 numBlocks
) {
	// LOGIC TO THE KERNEL COMPUTATION.
}

You can call this GPU function in host like this:

@lru_cache(maxsize=8)
def compile_function(code_filename: str, function_name: str) -> Callable:
	module = DynamicModule()
	with open(os.path.join(KERNEL_DIR, code_filename), "rb") as f:
	module.add_data(f.read(), jit_input_type.PTX, name="kernel.ptx")
	module.link()
return module.get_function(function_name)

Kernel 1 : Naive Implementation

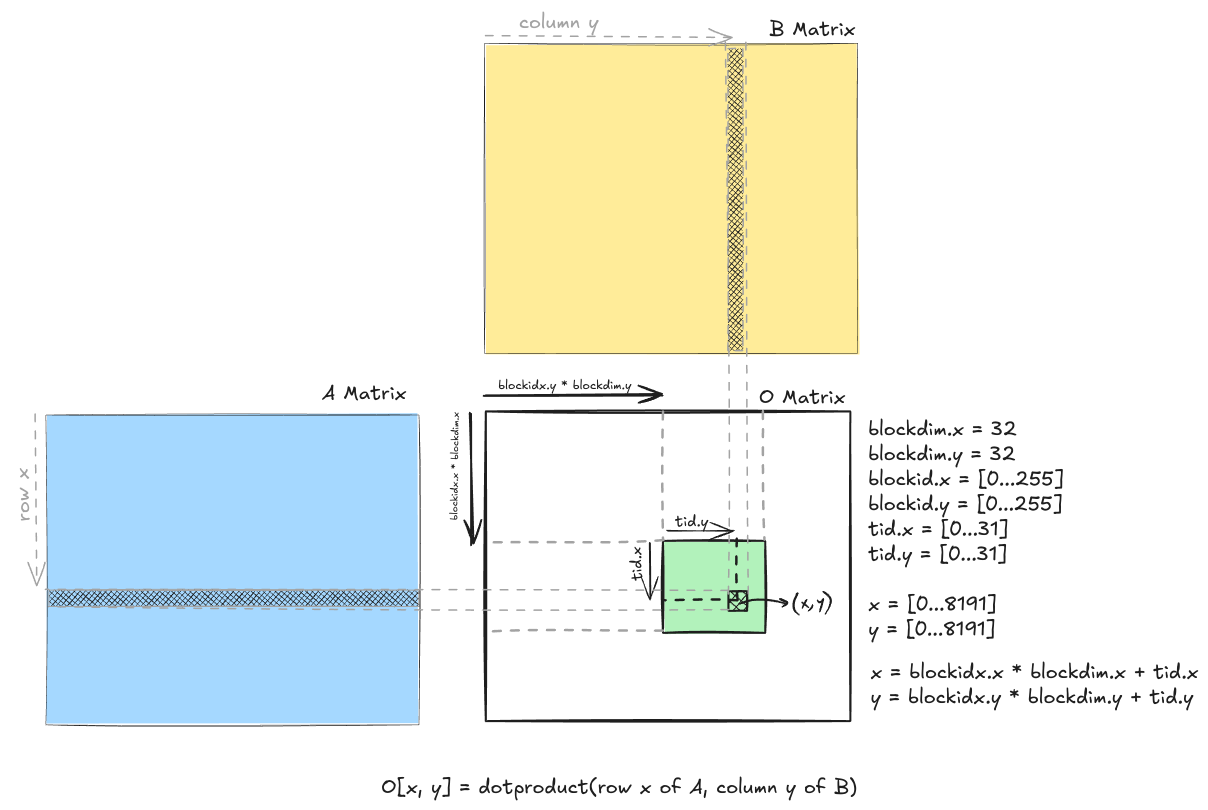
We have output matrix O, which has 8192 x 8192 elements. We create a grid of 256 x 256 blocks and each block has 32 x 32 threads. The goal of each thread is to compute the output of each element it maps to in the output matrix. If the thread corresponds to (x, y) index in matrix O. Then it performs dot product between rowA(x) and colB(y) to get the value of O(x, y). The image below visualizes the computation.

The code below gives us the full logic of the above computation.

.version 8.0
.target sm_86 
.address_size 64

.visible .entry sgemm_naive(
    .param .u64 ptrA,
    .param .u64 ptrB,
    .param .u64 ptrOut,
    .param .u32 numBlocks
) {
    // declaring registers for tid, bid, and bdim.
    .reg .u32 %t_id_x;
    .reg .u32 %t_id_y;
    .reg .u32 %b_dim_x;
    .reg .u32 %b_dim_y;
    .reg .u32 %b_id_x;
    .reg .u32 %b_id_y;

    // declaring registers for the indexing of row and col
    .reg .u32 %x;
    .reg .u32 %y;

    // accumulator register to store sums of mults.
    .reg .f32 %f_acc;

    // registers for the iterating loop
    .reg .s32 %i;
    .reg .pred %p;

    // registers to store the address of A, B, O
    .reg .u64 %r_ptrA;
    .reg .u64 %r_ptrB;
    .reg .u64 %r_ptrO;

    // registers which holds the value from A, B which are multiplied.
    .reg .f32 %val_a;
    .reg .f32 %val_b;
    .reg .f32 %val_res;

    // register for storing indexing array A, B and O.
    .reg .s32 %r_aidx;
    .reg .s32 %r_bidx;
    .reg .s32 %r_oidx;

    // register for holding the address of computations
    .reg .u64 %r_addr_a;
    .reg .u64 %r_addr_b;
    .reg .u64 %r_addr_o;

    // loading address form param state space (ss) to register ss.
    ld.param.u64 %r_ptrA, [ptrA];
    ld.param.u64 %r_ptrB, [ptrB];
    ld.param.u64 %r_ptrO, [ptrOut];

    // moving data from special registers to general purpose registers.
    mov.u32 %t_id_x, %tid.x;
    mov.u32 %t_id_y, %tid.y;
    mov.u32 %b_id_x, %ctaid.x;
    mov.u32 %b_id_y, %ctaid.y;
    mov.u32 %b_dim_x, %ntid.x;
    mov.u32 %b_dim_y, %ntid.y;

    // computing x, y
    // x = bid.x * bdim.x + tid.x
    // y = bid.y * bdim.y + tid.y
    mad.lo.u32 %x, %b_id_x, %b_dim_x, %t_id_x;
    mad.lo.u32 %y, %b_id_y, %b_dim_y, %t_id_y;

    // initializing acc to be zero
    mov.f32 %f_acc, 0.0; 
    mov.s32 %i, 0;

loop_start:
    setp.lt.s32 %p, %i, 8192;
    @!%p bra loop_end;

    // computing the A index -> x * 8192 + i
    mad.lo.s32 %r_aidx, %x, 8192, %i;
    mul.wide.s32 %r_addr_a, %r_aidx, 4;
    add.u64 %r_addr_a, %r_ptrA, %r_addr_a;

    // computing the B index -> i * 8192 + y
    mad.lo.s32 %r_bidx, %i, 8192, %y;
    mul.wide.s32 %r_addr_b, %r_bidx, 4;
    add.u64 %r_addr_b, %r_ptrB, %r_addr_b;

    // get A and B vals
    ld.global.f32 %val_a, [%r_addr_a];
    ld.global.f32 %val_b, [%r_addr_b];

    // perform multiplication
    mul.f32 %val_res, %val_a, %val_b; 
    add.f32 %f_acc, %f_acc, %val_res;

    add.s32 %i, %i, 1;
    bra loop_start;

loop_end:
    // store the result in O
    // computing the O index -> x * 8192 + y
    mad.lo.s32 %r_oidx, %x, 8192, %y;
    mul.wide.s32 %r_addr_o, %r_oidx, 4;
    add.u64 %r_addr_o, %r_ptrO, %r_addr_o;

    st.global.f32 [%r_addr_o], %f_acc; 
}

I have written the code in such a way that I declare all the needed registers, then moving the values to the registers and at last the computation. Register declaration is self-explanatory. Let us explore, some unique part of the code -

  • mov.u32 %t_id_x, %tid.x; : The %t_id_x is a u32 general purpose register, and it stores the value threadIdx.x. We can access this value using special register %tid.x. We are doing this mov because we cannot use special registers in instruction definition (ISA restriction). So we have to perform the transfer manually, which is what this statement does.
  • ld.param.u64 %r_ptrA, [ptrA]; : We are passing the pointer of data using function parameters, So this address for this data in parameter state space. We have to load this address in a u64 general purpose register if we want to compute and use the address in the instruction.
  • mad.lo.u32 %x, %b_id_x, %b_dim_x, %t_id_x; : This instruction performs multiply and add on integer type and computes the row x value.
  • The mentioned instruction performs comparison in loop and determines the control flow. This is performed using predicate registers. The set.lt.s32 %rd, %rs, val checks if %rs < val and stores the value in predicate register %p (the register should be declared like this .reg .pred %p;). The next like evaluates the predicate register, if it is true then it performs the branch instruction and moves to the end of the loop.
setp.lt.s32 %p, %i, 8192; 
@!%p bra loop_end;
  • Next is the address calculation to get the value from global memory. Values are stored in row major format.
    // computing the A index -> x * 8192 + i
    mad.lo.s32 %r_aidx, %x, 8192, %i; // computes x * col + i
    mul.wide.s32 %r_addr_a, %r_aidx, 4; // multiply by 4, f32 size is 4
    add.u64 %r_addr_a, %r_ptrA, %r_addr_a; // offset added to ptrA
  • This below instruction helps us load the data from global memory to local registers for computation:
    // get A and B vals
    ld.global.f32 %val_a, [%r_addr_a];
    ld.global.f32 %val_b, [%r_addr_b];
  • For storing the result from computation can be store from register to global memory using store instruction.
	st.global.f32 [%r_addr_o], %f_acc;

Performance numbers: Time: 15.64 s Speed up: 1.0

Kernel 2 : Global Memory Coalescing

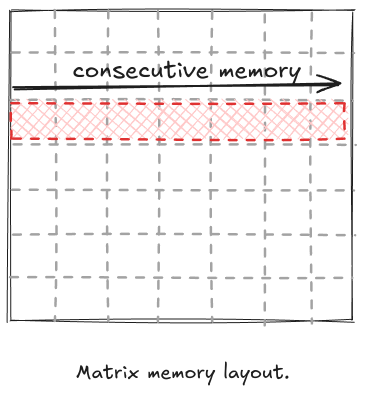
Let us see the memory access patterns of the above naive kernel. The memory of the array is taken in row major format by our implementation, which looks like the diagram given below.

We know that thread indexes are computed in the following way:

threadId = threadIdx.x+blockDim.x*(threadIdx.y+blockDim.y*threadIdx.z)

The thread along x direction are continuous, i.e. threads are numbered in row major form too. Now, let us see how the row and col for dot product is computed using thread id.

  x = blockIdx.x * blockDim.x + threadIdx.x;
  y = blockIdx.y * blockDim.y + threadIdx.y;

Since, threadIdx.x increases first, that dictates our next occurring thread in the warp. All the threads in warp are consecutive. To visualize how the memory is accessed by consecutive threads, let us assume we have a warp size of 4.

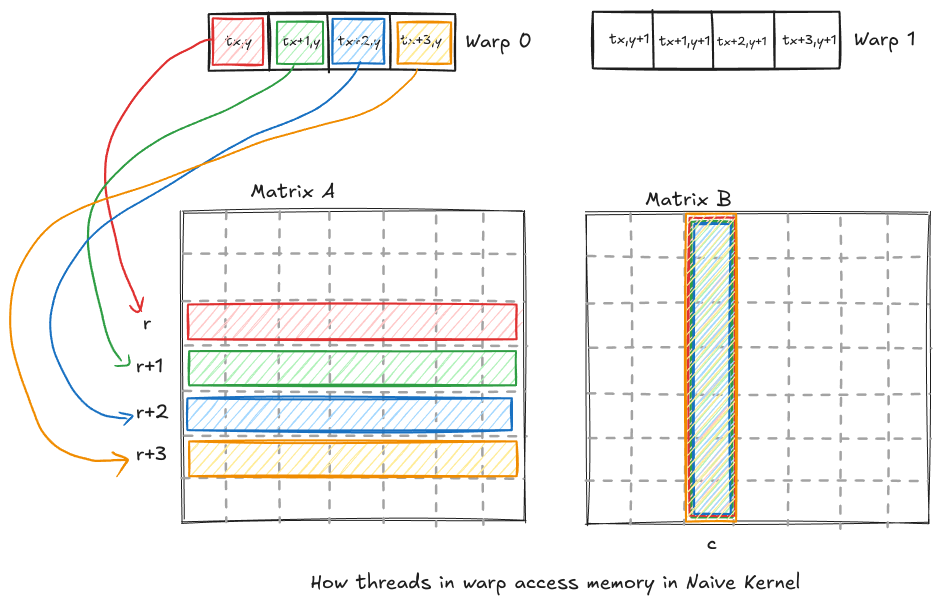
As you can see, the consecutive threads in a warp access different rows, which are not contiguous in our memory layout. Why is it important ? It is important because sequential memory accesses by threads that are part of the same warp can be grouped and executed as one. This is referred to as global memory coalescing. This reduces the number of memory instructions to global memory, reducing traffic and improving the performance. Now, how do we change the code in such a way that the threads in a warp access sequential memory. We can do this by making the threads along x dimension handle the columns of matrix B and threads along y dimension handle rows or columns of matrix A.

  x = blockIdx.y * blockDim.y + threadIdx.y;
  y = blockIdx.x * blockDim.x + threadIdx.x;

Let us see how the memory access looks like now.

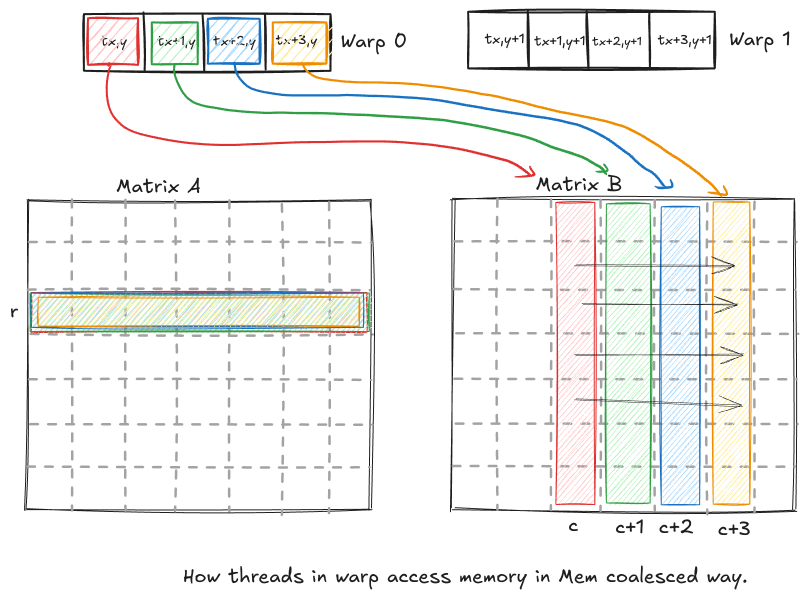As you can see the memory access by each thread is in consecutive way. The kernel code looks like this:

.version 8.0
.target sm_86 
.address_size 64

.visible .entry sgemm_mem_coalesce(
    .param .u64 ptrA,
    .param .u64 ptrB,
    .param .u64 ptrOut,
    .param .u32 numBlocks
) {
    // declaring registers for tid, bid, and bdim.
    .reg .u32 %t_id_x;
    .reg .u32 %t_id_y;
    .reg .u32 %b_dim_x;
    .reg .u32 %b_dim_y;
    .reg .u32 %b_id_x;
    .reg .u32 %b_id_y;

    // declaring registers to identify which thread we are using.
    .reg .u32 %x;
    .reg .u32 %y;

    // accumulator register to add part of dot product.
    .reg .f32 %f_acc;

    // registers for the loop
    .reg .s32 %i;
    .reg .pred %p;

    // registers to store the address of Array's
    .reg .u64 %r_ptrA;
    .reg .u64 %r_ptrB;
    .reg .u64 %r_ptrO;

    // the register which holds the value from A, B which are multiplied.
    .reg .f32 %val_a;
    .reg .f32 %val_b;
    .reg .f32 %val_res;

    // register for holding index of A and B array
    .reg .s32 %r_aidx;
    .reg .s32 %r_bidx;
    .reg .s32 %r_oidx;

    // register for holding the address of computation
    .reg .u64 %r_addr_a;
    .reg .u64 %r_addr_b;
    .reg .u64 %r_addr_o;

    // loading address form param state space (ss) to register ss.
    ld.param.u64 %r_ptrA, [ptrA];
    ld.param.u64 %r_ptrB, [ptrB];
    ld.param.u64 %r_ptrO, [ptrOut];

    // moving data from special registers to general purpose registers.
    mov.u32 %t_id_x, %tid.x;
    mov.u32 %t_id_y, %tid.y;
    mov.u32 %b_id_x, %ctaid.x;
    mov.u32 %b_id_y, %ctaid.y;
    mov.u32 %b_dim_x, %ntid.x;
    mov.u32 %b_dim_y, %ntid.y;

    // In naive kernel we used,
    //   row x using threads along x dimension.
    //   col y using threads along y dimension.
    // In memory coalesced we use,
    //   row x using threads along y dimension 
    //   col y using threads along x dimension
    mad.lo.u32 %x, %b_id_y, %b_dim_y, %t_id_y;
    mad.lo.u32 %y, %b_id_x, %b_dim_x, %t_id_x;

    // initializing acc to be zero
    mov.f32 %f_acc, 0.0; 
    mov.s32 %i, 0;

loop_start:
    setp.lt.s32 %p, %i, 8192;
    @!%p bra loop_end;

    // computing the A index -> x * 8192 + i
    mad.lo.s32 %r_aidx, %x, 8192, %i;
    mul.wide.s32 %r_addr_a, %r_aidx, 4;
    add.u64 %r_addr_a, %r_ptrA, %r_addr_a;

    // computing the B index -> i * 8192 + y
    mad.lo.s32 %r_bidx, %i, 8192, %y;
    mul.wide.s32 %r_addr_b, %r_bidx, 4;
    add.u64 %r_addr_b, %r_ptrB, %r_addr_b;

    // get A and B vals
    ld.global.f32 %val_a, [%r_addr_a];
    ld.global.f32 %val_b, [%r_addr_b];

    // perform multiplication
    mul.f32 %val_res, %val_a, %val_b; 
    add.f32 %f_acc, %f_acc, %val_res;

    add.s32 %i, %i, 1;
    bra loop_start;

loop_end:
    // store the result in O
    // computing the O index -> x * 8192 + y
    mad.lo.s32 %r_oidx, %x, 8192, %y;
    mul.wide.s32 %r_addr_o, %r_oidx, 4;
    add.u64 %r_addr_o, %r_ptrO, %r_addr_o;

    st.global.f32 [%r_addr_o], %f_acc; 
}

Performance numbers: Time: 8.62s Speed up: 1.81

We got good speed up! Next let us see if we improve memory access even better.

Kernel 3 : Shared Memory Cache-Blocking

Before going into this kernel, let us first understand how the GPU hardware works. GPU is a collection of Streaming Multiprocessors (SM). Each SM can execute multiple blocks (note, not a partial block of threads). Each SM consist of scalar processors (SPs) which executes threads in warps. The warps are scheduled using warp scheduler. One more unique this about SMs is that it has a faster memory called shared memory which the threads in same block can access together. The shared memory bandwidth is way bigger than global memory bandwidth (almost two orders of magnitude big).

Now when we look at our kernel, we can see that we access the same row and column multiple times, resulting in repeated memory calls to global memory. So, instead of doing that, why not load a chunk (or tile) of global memory to shared memory initially. Then store the partial dot product computed using these chunks and move the tile to get the complete result, and then store the output. This not only reduces the global memory requests, it also max utilizes the shared memory bandwidth by fulling the repeated row, col memory access.

Now let us visualize this computation:

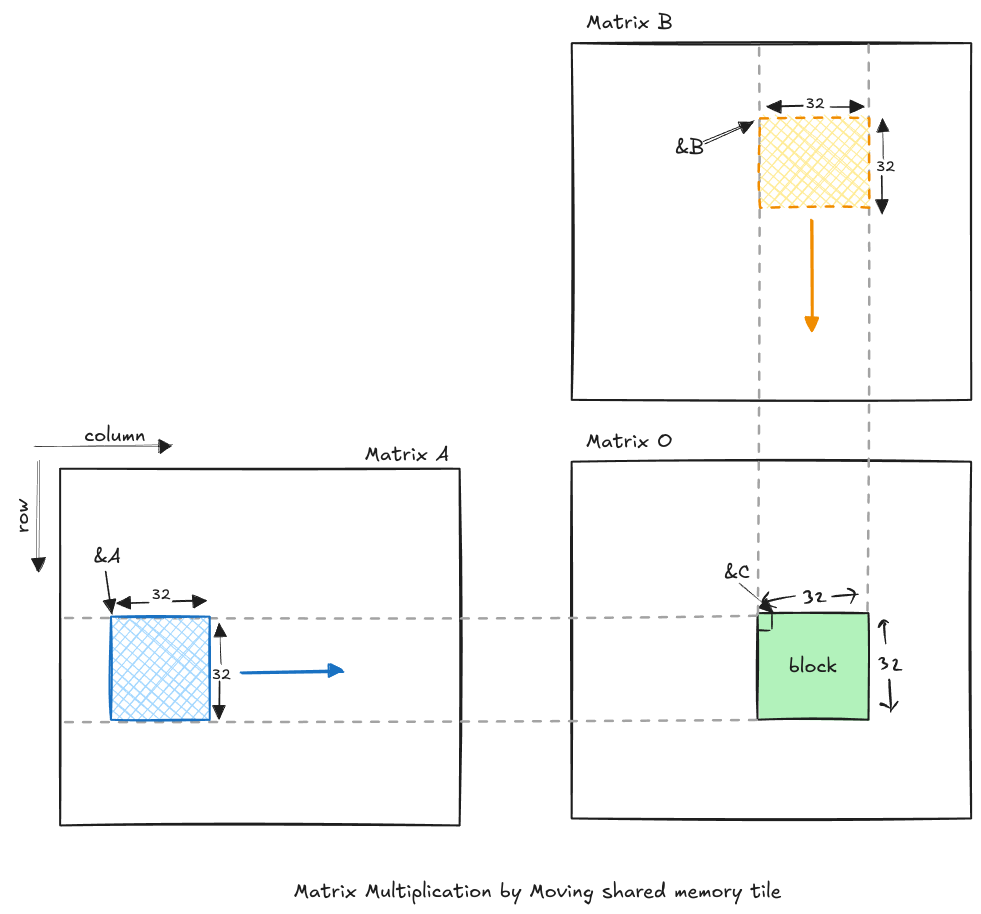
Code:

.version 8.0
.target sm_86 
.address_size 64

.visible .entry sgemm_shmem_blocking(
    .param .u64 ptrA,
    .param .u64 ptrB,
    .param .u64 ptrOut,
    .param .u32 numBlocks
) {

    // declaring shared memory to implement blocking
    .shared .align 4 .f32 As[1024];
    .shared .align 4 .f32 Bs[1024];

    // declaring registers for tid, bid, and bdim.
    .reg .u32 %t_id_x;
    .reg .u32 %t_id_y;
    .reg .u32 %b_dim_x;
    .reg .u32 %b_dim_y;
    .reg .u32 %b_id_x;
    .reg .u32 %b_id_y;

    // declaring registers to identify which thread we are using.
    .reg .u32 %x;
    .reg .u32 %y;

    // threadid inside the block. 
    .reg .u32 %tr;
    .reg .u32 %tc;

    // register to hold blockssize;
    .reg .u32 %BS;

    // accumulator register to add part of dot product.
    .reg .f32 %f_acc;

    // registers for the loop
    .reg .s32 %i;
    .reg .s32 %dotid;
    .reg .pred %p;

    // registers to store the address of Array's
    .reg .u64 %r_ptrA;
    .reg .u64 %r_ptrB;
    .reg .u64 %r_ptrO;

    // testing
    .reg .u64 %r_A;
    .reg .u64 %r_B;
    .reg .u64 %r_O;

    .reg .u32 %r_As;
    .reg .u32 %r_Bs;

    // the register which holds the value from A, B which are multiplied.
    .reg .f32 %val_a;
    .reg .f32 %val_b;
    .reg .f32 %val_res;

    // register for holding index of A and B array
    .reg .s32 %r_aidx;
    .reg .s32 %r_bidx;
    .reg .s32 %r_oidx;

    .reg .s32 %r_asidx;
    .reg .s32 %r_bsidx;

    // register for holding the address of computation
    .reg .u64 %r_addr_a;
    .reg .u64 %r_addr_b;
    .reg .u64 %r_addr_o;

    .reg .u32 %r_addr_as;
    .reg .u32 %r_addr_bs;

    // temp regisers
    .reg .u64 %temp_u64;

    // BS := 32
    mov.u32 %BS, 32;

    // loading address form param state space (ss) to register ss.
    ld.param.u64 %r_ptrA, [ptrA];
    ld.param.u64 %r_ptrB, [ptrB];
    ld.param.u64 %r_ptrO, [ptrOut];

    mov.u32 %r_As, As;
    mov.u32 %r_Bs, Bs;


    // moving data from special registers to general purpose registers.
    mov.u32 %t_id_x, %tid.x;
    mov.u32 %t_id_y, %tid.y;
    mov.u32 %b_id_x, %ctaid.x;
    mov.u32 %b_id_y, %ctaid.y;
    mov.u32 %b_dim_x, %ntid.x;
    mov.u32 %b_dim_y, %ntid.y;

    mov.u32 %tr, %tid.y;
    mov.u32 %tc, %tid.x;

    // A = ptrA + 4*(bid.x * BS * 8192)
    mul.lo.s32 %r_aidx, %b_id_x, %BS;
    mul.lo.s32 %r_aidx, %r_aidx, 8192;
    mul.wide.s32 %r_A, %r_aidx, 4;
    add.u64 %r_A, %r_A, %r_ptrA; 

    // B = ptrB + 4*(bid.y * BS)
    mul.lo.s32 %r_bidx, %b_id_y, %BS;
    mul.wide.u32 %r_B, %r_bidx, 4;
    add.u64 %r_B, %r_B, %r_ptrB;

    // O = ptrO = 4*(bid.x*BS*8192 + bid.y * BS); 
    add.s32 %r_oidx, %r_aidx, %r_bidx;
    mul.wide.s32 %r_O, %r_oidx, 4;
    add.u64 %r_O, %r_O, %r_ptrO;

    // getting the x and y -> row(x) and row(y);
    mad.lo.u32 %y, %b_id_y, %b_dim_y, %t_id_y;
    mad.lo.u32 %x, %b_id_x, %b_dim_x, %t_id_x;

    // initializing acc to be zero
    mov.f32 %f_acc, 0.0; 
    mov.s32 %i, 0;

loop_start:
    setp.lt.s32 %p, %i, 8192;
    @!%p bra loop_end;

    // loads the 32x32 from A, B ----> shared memory
    // performing As[tr*BS + tc] = A[tr*8192 + tc]
    mad.lo.s32 %r_asidx, %tr, 32, %tc;
    mul.lo.u32 %r_addr_as, %r_asidx, 4;
    add.u32 %r_addr_as, %r_addr_as, %r_As;

    mad.lo.s32 %r_aidx, %tr, 8192, %tc;
    mul.wide.s32 %r_addr_a, %r_aidx, 4;
    add.u64 %r_addr_a, %r_A, %r_addr_a; 

    ld.global.f32 %val_a, [%r_addr_a];
    st.shared.f32 [%r_addr_as], %val_a;

    // performing Bs[tr*BS + tc] = B[tr*8192 + tc]
    mad.lo.s32 %r_bsidx, %tr, 32, %tc;
    mul.lo.u32 %r_addr_bs, %r_bsidx, 4;
    add.u32 %r_addr_bs, %r_addr_bs, %r_Bs;

    mad.lo.s32 %r_bidx, %tr, 8192, %tc;
    mul.wide.s32 %r_addr_b, %r_bidx, 4;
    add.u64 %r_addr_b, %r_B, %r_addr_b; 

    ld.global.f32 %val_b, [%r_addr_b];
    st.shared.f32 [%r_addr_bs], %val_b;

    // sync call
    bar.sync 0;

    // updating the A and B address to move the 32x32 window.
    // r_A := r_A + 4*BS
    // r_B := r_B + 4*(BS * 8192)
    // mad.lo.u64 %r_A, 32, 4, %r_A;
    add.u64 %r_A, %r_A, 128;
    add.u64 %r_B, %r_B, 1048576;

    mov.s32 %dotid, 0;
    inner_loop_start:    
        setp.lt.s32 %p, %dotid, 32;
        @!%p bra inner_loop_end;

        // As[tr*BS + dotid] 
        mad.lo.s32 %r_asidx, %tr, %BS, %dotid; 
        mul.lo.u32 %r_addr_as, %r_asidx, 4;
        add.u32 %r_addr_as, %r_addr_as, %r_As;

        
        // Bs[dotid*BS + tc]
        mad.lo.s32 %r_bsidx, %dotid, %BS, %tc; 
        mul.lo.u32 %r_addr_bs, %r_bsidx, 4;
        add.u32 %r_addr_bs, %r_addr_bs, %r_Bs;

        ld.shared.f32 %val_a, [%r_addr_as];
        ld.shared.f32 %val_b, [%r_addr_bs];
        
        mul.f32 %val_res, %val_a, %val_b;
        add.f32 %f_acc, %f_acc, %val_res;

        add.s32 %dotid, %dotid, 1;
        bra inner_loop_start;

    inner_loop_end:

    // sync call
    bar.sync 0;

    add.s32 %i, %i, 32;
    bra loop_start;

loop_end:
    // store the result in O
    mad.lo.s32 %r_oidx, %tr, 8192, %tc;
    mul.wide.s32 %r_addr_o, %r_oidx, 4;
    add.u64 %r_addr_o, %r_O, %r_addr_o;

    st.global.f32 [%r_addr_o], %f_acc; 
}

Some unique introduction to our ptx code:

  • Synchronization:
  • Shared Memory:
  • Accessing Shared memory:

Performance Numbers: Time: 2.44s Speed up: 6.40

Wow, we have really got such a significant speed-up.

Kernel 4 : 1D Block Tiling, multiple computation per thread.

Wow, we have done so much. But there are lot more optimization that can be done. We can visualize the bottlenecks using profiling tools like Nvidia Nsight etc. The next major bottlenecks we can see that is, we are doing a lot of memory calls to shared memory, this results in lot of threads waiting for memory access request than to perform computation. So, what we can do is that instead of one thread computing one output, it computes multiple outputs. This means, we reduce the number of threads needed per block and also reduce the shared memory size. We can do this by loading less global memory in shared memory, and also make sure each block computes more results than the number of threads in the block.

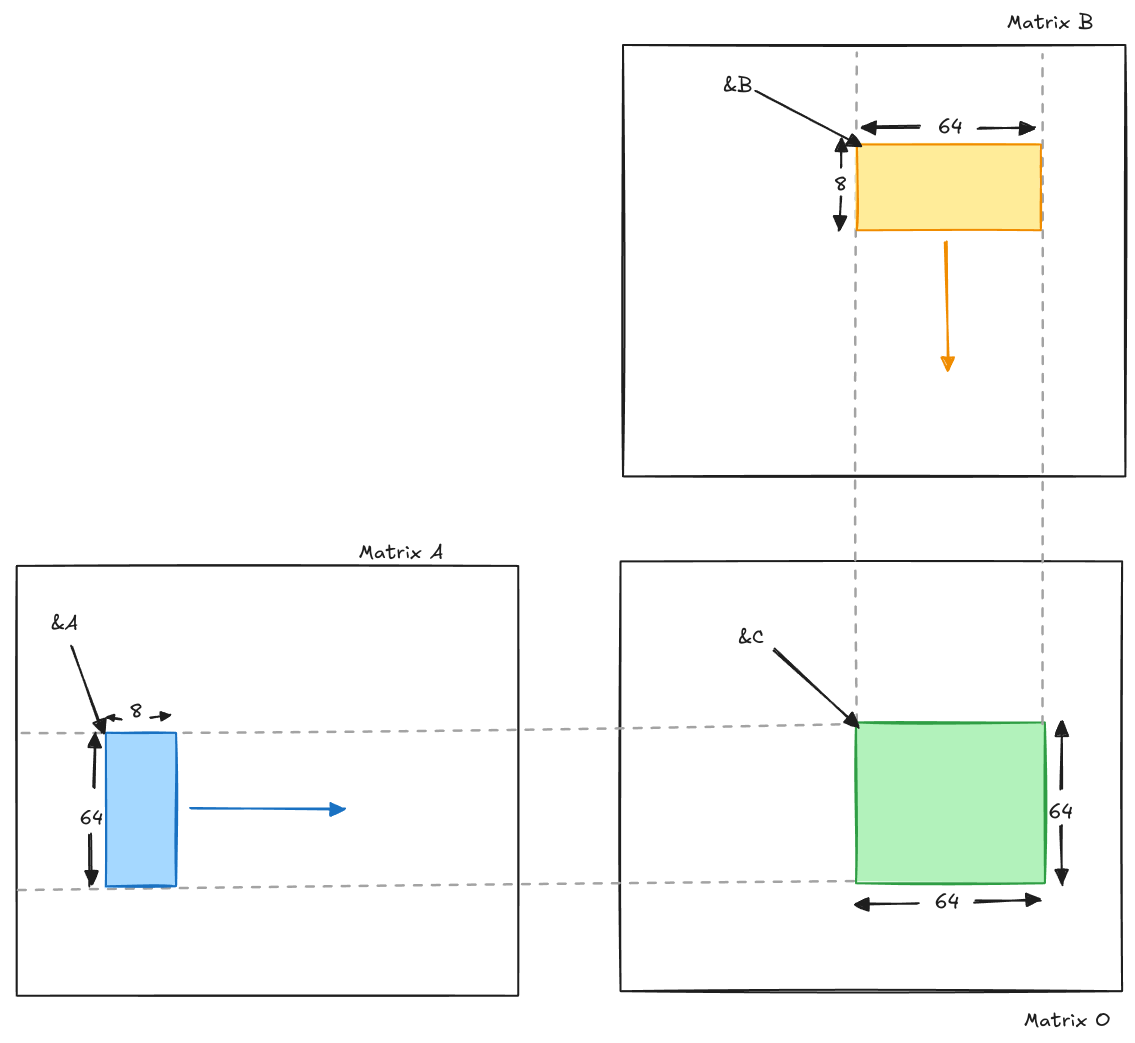
Let us visualize how we break down the problem: We have Output Matrix of size: 8192 x 8192. Let us divide this matrix in smaller chunks of size : 64x64 = 4096. Change logic, so each thread in a block computes 8 output results, so the number of threads per block = 512 = (4096/8).

Number of blocks in the grid = (8192x8192) / (64x64) = 16284

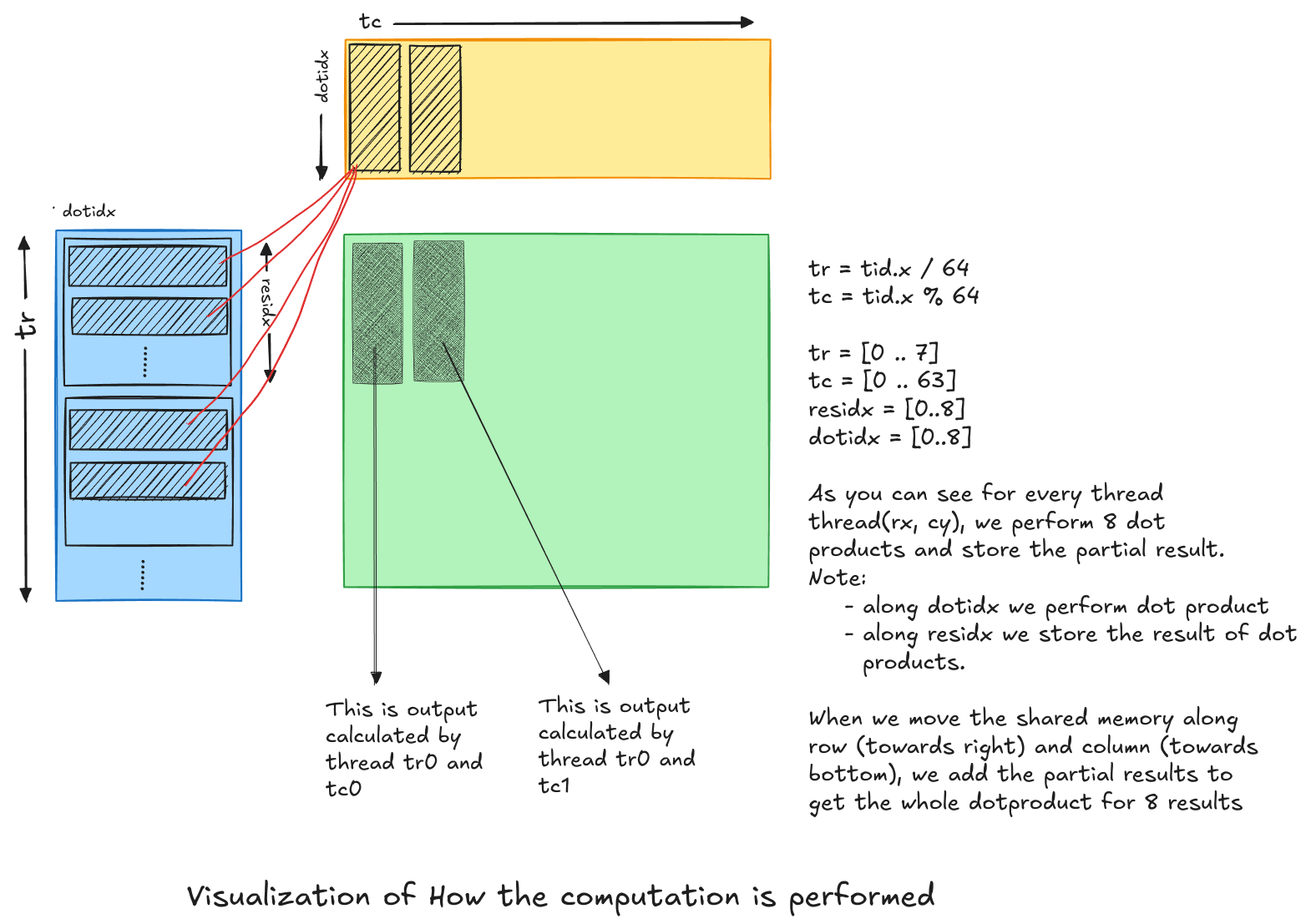
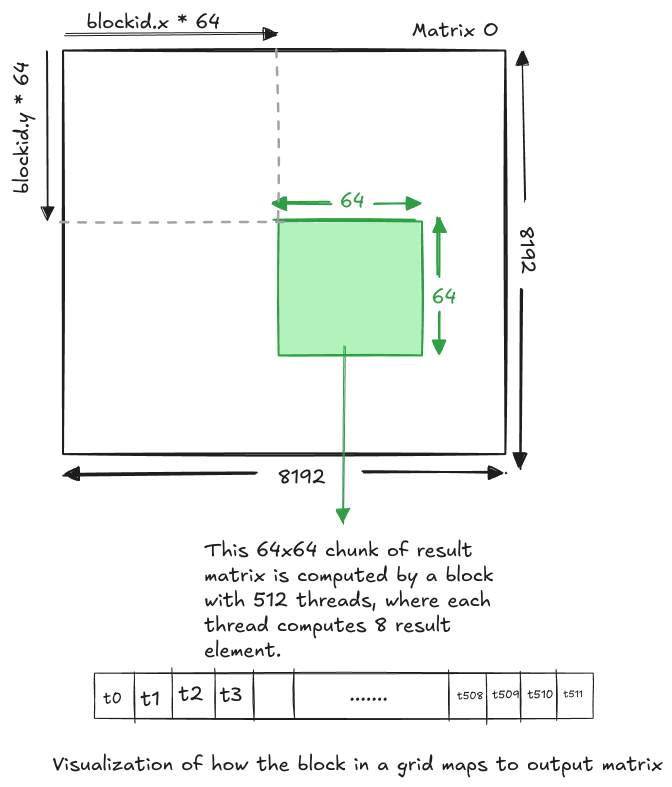How do we use 512 threads in a block to compute 4096 elements in the chunk. We will use the same moving shared memory approach. Instead of storing all 64x64 chunk of A & B in shared memory, we reduce the length along moving dimension by factor of 8. That is, we use 64x8 (for A matrix) + 8x64 (for B matrix). Let us see how we use these shared memory to compute the chunk.

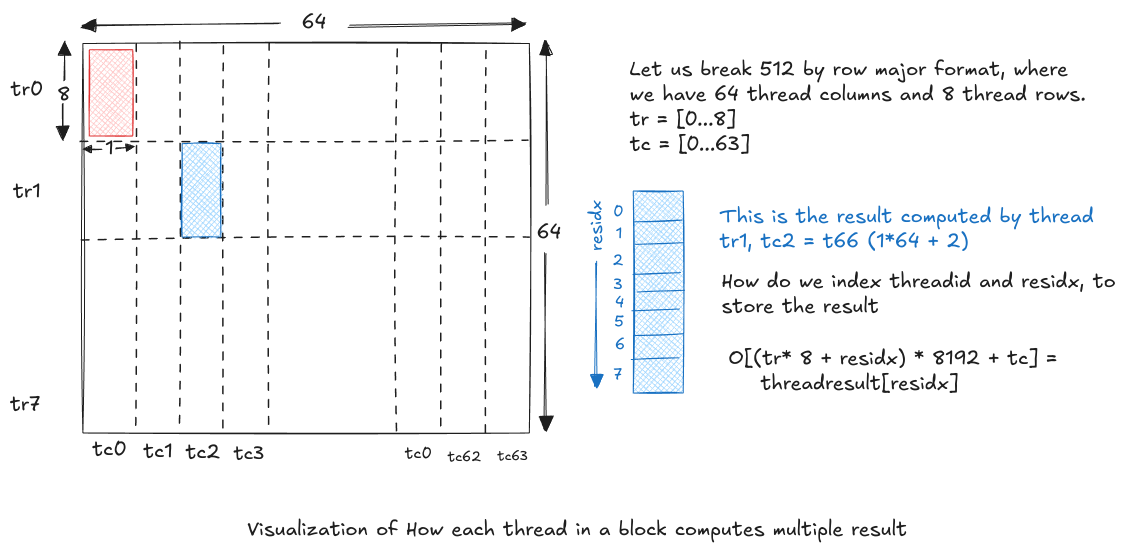
Given below drawing, tells how we perform inner loop to compute the multiple results:

Code:

.version 8.0
.target sm_86 
.address_size 64


/*
I am using following constants

block size = 512 (1D)
We split the 8196x8196 into smaller units of 64x64.
Where each block is responsilbe to compute 64x64 = (4096)

Since, each block has 512 threads, each thread has to compute multiple output
element. Each thread has to compute 8 outputs (4096/512).

BN = 64
BK = 8
BT = 8
*/

.visible .entry sgemm_shmem_1dblocktiling(
    .param .u64 ptrA,
    .param .u64 ptrB,
    .param .u64 ptrOut
) {

    // declaring shared memory to implement blocking
    // Each block of A, B is of shape (64x8) and (8x64) respectively
    .shared .align 4 .f32 As[512];
    .shared .align 4 .f32 Bs[512];

    // declaring registers for tid, bid, and bdim.
    .reg .u32 %t_id_x;
    .reg .u32 %t_id_y;
    .reg .u32 %b_dim_x;
    .reg .u32 %b_dim_y;
    .reg .u32 %b_id_x;
    .reg .u32 %b_id_y;

    // threadid inside the block. 
    .reg .u32 %tr;
    .reg .u32 %tc;
    .reg .u32 %irA; // inner_row A
    .reg .u32 %irB; // inner_row B
    .reg .u32 %icA; // inner_col A
    .reg .u32 %icB; // inner_col B

    // register to hold blockssize;
    .reg .u32 %BN;
    .reg .u32 %TM;
    .reg .u32 %BK;

    // register to store the coloum value
    .reg .f32 %btmp;

    // to store the multiple output computation by a thread.
    .reg .f32 %thread_result<8>;

    // registers for the loop
    .reg .s32 %i; // for moving the A, B blocks right and bottom respc.
    .reg .s32 %dotid; // to move downward of B block
    .reg .pred %p;

    // registers to store the address of Array's
    .reg .u64 %r_ptrA;
    .reg .u64 %r_ptrB;
    .reg .u64 %r_ptrO;

    // testing
    .reg .u64 %r_A;
    .reg .u64 %r_B;
    .reg .u64 %r_O;

    .reg .u32 %r_As;
    .reg .u32 %r_Bs;

    // the register which holds the value from A, B which are multiplied.
    .reg .f32 %val_a;
    .reg .f32 %val_b;
    .reg .f32 %val_res;

    // register for holding index of A and B array
    .reg .u32 %r_aidx;
    .reg .u32 %r_bidx;
    .reg .u32 %r_oidx;

    .reg .u32 %r_asidx;
    .reg .u32 %r_bsidx;

    // register for holding the address of computation
    .reg .u64 %r_addr_a;
    .reg .u64 %r_addr_b;
    .reg .u64 %r_addr_o;

    .reg .u32 %r_addr_as;
    .reg .u32 %r_addr_bs;

    // temp regisers
    .reg .u64 %temp_u64;
    .reg .u32 %temp_u32;

    // populating the constants;
    mov.u32 %BN, 64;
    mov.u32 %BK, 8;
    mov.u32 %TM, 8;


    // init thread results to 0;
    mov.f32 %thread_result0, 0.0;
    mov.f32 %thread_result1, 0.0;
    mov.f32 %thread_result2, 0.0;
    mov.f32 %thread_result3, 0.0;
    mov.f32 %thread_result4, 0.0;
    mov.f32 %thread_result5, 0.0;
    mov.f32 %thread_result6, 0.0;
    mov.f32 %thread_result7, 0.0;

    // loading address form param state space (ss) to register ss.
    ld.param.u64 %r_ptrA, [ptrA];
    ld.param.u64 %r_ptrB, [ptrB];
    ld.param.u64 %r_ptrO, [ptrOut];

    // loading the address of shared memory.
    mov.u32 %r_As, As;
    mov.u32 %r_Bs, Bs;


    // moving data from special registers to general purpose registers.
    mov.u32 %t_id_x, %tid.x;
    mov.u32 %b_id_x, %ctaid.x;
    mov.u32 %b_id_y, %ctaid.y;
    mov.u32 %b_dim_x, %ntid.x;

    // computing tr, ta
    div.u32 %tr, %t_id_x, %BN;
    rem.u32 %tc, %t_id_x, %BN;

    // computing irA, irB, icA, icB -> used for indexing inner loop
    div.u32 %irA, %t_id_x, %BK;
    rem.u32 %icA, %t_id_x, %BK;
    div.u32 %irB, %t_id_x, %BN;
    rem.u32 %icB, %t_id_x, %BN;

    // A = ptrA + 4*(bid.x * BN * 8192)
    mul.lo.u32 %r_aidx, %b_id_x, %BN;
    mul.lo.u32 %r_aidx, %r_aidx, 8192;
    mul.wide.u32 %r_A, %r_aidx, 4;
    add.u64 %r_A, %r_A, %r_ptrA; 

    // B = ptrB + 4*(bid.y * BN)
    mul.lo.u32 %r_bidx, %b_id_y, %BN;
    mul.wide.u32 %r_B, %r_bidx, 4;
    add.u64 %r_B, %r_B, %r_ptrB;

    // O = ptrO = 4*(bid.x*BN*8192 + bid.y * BN); 
    add.u32 %r_oidx, %r_aidx, %r_bidx;
    mul.wide.u32 %r_O, %r_oidx, 4;
    add.u64 %r_O, %r_O, %r_ptrO;

    // initializing acc to be zero
    mov.s32 %i, 0;

    // loop to move the A block towards right and B block towards left
loop_start:
    setp.lt.s32 %p, %i, 8192;
    @!%p bra loop_end;

    // loads the (64x8), (8x64) from A, B ----> shared memory As, Bs
    // BK = 8, N = 8192
    // performing As[irA*8 + icA] = A[irA*8192 + icA]
    mad.lo.u32 %r_asidx, %irA, 8, %icA;
    mul.lo.u32 %r_addr_as, %r_asidx, 4;
    add.u32 %r_addr_as, %r_addr_as, %r_As;

    mad.lo.u32 %r_aidx, %irA, 8192, %icA;
    mul.wide.s32 %r_addr_a, %r_aidx, 4;
    add.u64 %r_addr_a, %r_A, %r_addr_a; 

    ld.global.f32 %val_a, [%r_addr_a];
    st.shared.f32 [%r_addr_as], %val_a;

    // performing Bs[irB*64 + icB] = B[irB*8192 + icB]
    mad.lo.u32 %r_bsidx, %irB, 64, %icB;
    mul.lo.u32 %r_addr_bs, %r_bsidx, 4;
    add.u32 %r_addr_bs, %r_addr_bs, %r_Bs;

    mad.lo.u32 %r_bidx, %irB, 8192, %icB;
    mul.wide.s32 %r_addr_b, %r_bidx, 4;
    add.u64 %r_addr_b, %r_B, %r_addr_b; 

    ld.global.f32 %val_b, [%r_addr_b];
    st.shared.f32 [%r_addr_bs], %val_b;

    // sync call
    bar.sync 0;

    // updating the A and B address to move the 32x32 window.
    // r_A := r_A + 4*BK
    // r_B := r_B + 4*(BK * 8192)
    add.u64 %r_A, %r_A, 32;
    add.u64 %r_B, %r_B, 262144;


    // loop which moves down inside B across each column
    mov.u32 %dotid, 0;
    loop_inner_B_start:
        setp.lt.s32 %p, %dotid, %BK;
        @!%p bra loop_inner_B_end;

        // loading btmp := Bs[dotidx * BN + tc]
        mad.lo.u32 %r_bsidx, %dotid, %BN, %tc;
        mul.lo.u32 %r_addr_bs, %r_bsidx, 4;
        add.u32 %r_addr_bs, %r_addr_bs, %r_Bs;

        ld.shared.f32 %val_b, [%r_addr_bs];

        // unrolled loop for moving across each row downwards to
        // compute multiple results 
        // val_a := As[(tr*TM + residx)*BK + dotidx]
        mad.lo.u32 %temp_u32, %tr, %TM, 0;
        mad.lo.u32 %r_asidx, %temp_u32, %BK, %dotid;
        mul.lo.u32 %r_addr_as, %r_asidx, 4;
        add.u32 %r_addr_as, %r_addr_as, %r_As;

        ld.shared.f32 %val_a, [%r_addr_as];
        fma.rn.f32 %thread_result0, %val_a, %val_b, %thread_result0;
        // increamenting Bs addr by 4*BK (equivalent to incrementing residx)
        add.u32 %r_addr_as, %r_addr_as, 32;
        ld.shared.f32 %val_a, [%r_addr_as];
        fma.rn.f32 %thread_result1, %val_a, %val_b, %thread_result1;
        add.u32 %r_addr_as, %r_addr_as, 32;
        ld.shared.f32 %val_a, [%r_addr_as];
        fma.rn.f32 %thread_result2, %val_a, %val_b, %thread_result2;
        add.u32 %r_addr_as, %r_addr_as, 32;
        ld.shared.f32 %val_a, [%r_addr_as];
        fma.rn.f32 %thread_result3, %val_a, %val_b, %thread_result3;
        add.u32 %r_addr_as, %r_addr_as, 32;
        ld.shared.f32 %val_a, [%r_addr_as];
        fma.rn.f32 %thread_result4, %val_a, %val_b, %thread_result4;
        add.u32 %r_addr_as, %r_addr_as, 32;
        ld.shared.f32 %val_a, [%r_addr_as];
        fma.rn.f32 %thread_result5, %val_a, %val_b, %thread_result5;
        add.u32 %r_addr_as, %r_addr_as, 32;
        ld.shared.f32 %val_a, [%r_addr_as];
        fma.rn.f32 %thread_result6, %val_a, %val_b, %thread_result6;
        add.u32 %r_addr_as, %r_addr_as, 32;
        ld.shared.f32 %val_a, [%r_addr_as];
        fma.rn.f32 %thread_result7, %val_a, %val_b, %thread_result7;


        add.s32 %dotid, %dotid, 1;
        bra loop_inner_B_start;

    loop_inner_B_end:

    bar.sync 0;
    add.s32 %i, %i, 8;
    bra loop_start;

loop_end:
    // store the result in O
    mad.lo.s32 %temp_u32, %tr, %TM, 0;
    mad.lo.s32 %r_oidx, %temp_u32, 8192, %tc;
    mul.wide.s32 %r_addr_o, %r_oidx, 4;
    add.u64 %r_addr_o, %r_O, %r_addr_o;

    st.global.f32 [%r_addr_o], %thread_result0; 

    add.u64 %r_addr_o, %r_addr_o, 32768;
    st.global.f32 [%r_addr_o], %thread_result1; 
    add.u64 %r_addr_o, %r_addr_o, 32768;
    st.global.f32 [%r_addr_o], %thread_result2; 
    add.u64 %r_addr_o, %r_addr_o, 32768;
    st.global.f32 [%r_addr_o], %thread_result3; 
    add.u64 %r_addr_o, %r_addr_o, 32768;
    st.global.f32 [%r_addr_o], %thread_result4; 
    add.u64 %r_addr_o, %r_addr_o, 32768;
    st.global.f32 [%r_addr_o], %thread_result5; 
    add.u64 %r_addr_o, %r_addr_o, 32768;
    st.global.f32 [%r_addr_o], %thread_result6; 
    add.u64 %r_addr_o, %r_addr_o, 32768;
    st.global.f32 [%r_addr_o], %thread_result7; 

}

Performance Numbers: Time: 1.24s Speed up: 12.62

There are a lot of optimization that can done further like we can reduce the shared memory access further by tiling it further along the other dimension as well. Also, we can vectorize the global and shared memory access. This will be tough to implement on pure ptx level, code. Maybe implementing custom compiler for generating these could be an interesting project (similar to Triton by with different trade-offs).

References

  • The kernel logic and understanding of the computation is thanks to the following blog post by Siboehm, here.
  • Skeleton code for compiling from ptx from Alex Nichol, here.
  • CUDA PTX handbook was helpful with syntax and general basic understanding of PTX, here