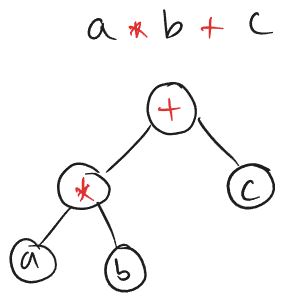
For the past couple of weeks, I was trying to write an interpreter in c++. One of the challenging aspects was generating the abstract syntax tree (AST). The one particular problem which was interesting is solving for operation precedence to generate correct abstract syntax tree. For example,
a * b + c = ((a * b) + c)
a + b * c = (a + (b * c))
You can see that we cannot do a+b before multiplying as it defies the precedence of operation in computation. The operator with highers precedence should ‘sink’ to the bottom of the AST. If the operator is at the bottom of the syntax tree, those are evaluated first.
Parsing and the problem of left recursion
There are many parsing techniques, but one of the simplest one is recursive descent parser. In this parsing technique, we have a set of mutually exclusive recursive functions which handles creation of nodes in AST, and we call recursive functions of the children connections based on patterns in tokens.
Let us take a simple grammar for parsing,
S -> S + Int | Int
The way we do it in recursive descent parsing is :
def S(p: Parser):
S(p)
p.expect(PLUS)
p.expect(INT)
Now you can see the problem already. This recursive function is called infinitely and causes stack overflow. This is the problem of ’left recursion’. Based on this, we have a plethora of processing that can be done to grammar to remove this left recursion and compiler books introduce LR parsing technique (which I have forgotten since my undergrad).
But the Pratt parsing solves this limitation of recursive descent problem using a simple modification to recursion. This solution honestly looks so simple but so cool.
Pratt Parsing
The Pratt parsing modified the Recursive descent parser to include a loop in its recursion. This transforms these too simple of recursive descent to have a kind of complex recursive calls. How does it look ?
def parse_expr():
...
while():
...
parse_expr()
...
...
This simple modification not just solves left recursion, but it also tackles the problem of precedence (associativity).
How does it solve left recursion?
Before calling the recursion, we have a condition in while loop, which it has to satisfy. If we put the terminating condition of a sentence (of a grammar) there, then this solves the problem of infinite recursion. But now, you may wonder why not just add the same condition in a if condition and let recursion handle the parsing. This is because if a function call ends then it ends, there is no handling of fallback due to operation precedence etc.
How do we solve the associativity of operators ?
We terminate the loop when we encounter not just termination of sentence, but also when we encounter operator whose precedence does not match. This make sure we end the current recursion and makes the current sub-tree independent and gives control back to the loop which called the recursion and handles the operation precedence by ‘sinking’ the higher precedent operator deeper into the AST.
The following is my function that implements the Pratt Parsing:
unique_ptr<Expression> Parser::parse_expression(int precedence = 0){
auto prefix = prefix_parse_fns[cur_token.type];
if(prefix == nullptr){
errors.push_back(fmt::format("no prefix parse function found \
for{} found\n", lexer::enum_to_string(cur_token.type)));
return nullptr;
}
auto left_expr = prefix();
while(!_peek_tok_is(lexer::TokenType::SEMICOLON) &&
precedence < _peek_precedence()){
auto infix = infix_parse_fns[peek_token.type];
if(infix == nullptr){
return left_expr;
}
next_token();
left_expr = infix(std::move(left_expr));
}
return left_expr;
}
Few things to note:
prefix_parse_fnsandinfix_parse_fnsjust returnsstd::functionfor the appropriate ‘mutually exclusive parse functions’ based on token (from lexer) encountered. This functional object is called.prefixoperators have higher precedence overinfixoperators, and also we treat parsing identifiers and integrals as prefix parsing (convenience).- Each parsing expression call has a precedence value as argument giving the precedence of operator that was parsed which resulted in this recursive call.